Seite 1 von 1
GamePad-Werte in korrekten Kreis umrechnen
Verfasst: 12.04.2013, 13:26
von Schrompf
Hallo Leute!
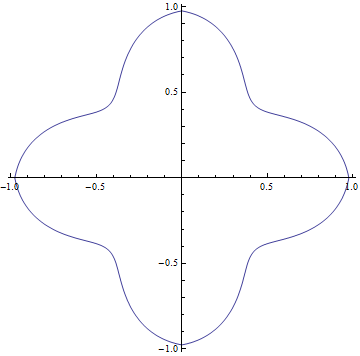
Ein potentiell banales Problem heute: ich habe einen XBox-Controller. Ich vermute aber, dass das Problem bei anderen GamePads das Gleiche ist. Da sind ja zwei Sticks drauf, die man analog auslenken kann. Deren Bewegungsspielraum sieht kreisförmig aus:

- pad_beispiel1.png (4.26 KiB) 2428 mal betrachtet
Von XInput, DirectInput oder was auch immer bekomme ich nun aber zwei separate Achsen, deren Werte sich jeweils im Bereich -0.45 bis +0.45 oder so bewegen. Und irgendwas auf dem Weg vom physikalischen Stick auf dem Controller bis in mein Programm rechnet die Werte so um, dass ich statt eines Kreises ein Rechteck bekomme. Also etwa so:
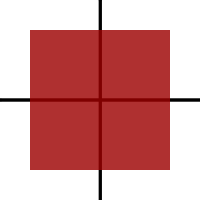
- pad_beispiel2.png (794 Bytes) 2430 mal betrachtet
Das kann ich sicherlich mathematisch irgendwie wieder ausgleichen. Aber ich stehe gerade auf dem Schlauch, wie ich das tun könnte, ohne den Betrag des Auslenkungsvektors zu verlieren. Hat jemand eine Idee?
Bye, Thomas
Re: GamePad-Werte in korrekten Kreis umrechnen
Verfasst: 12.04.2013, 13:44
von CodingCat
Eine naheliegende Möglichkeit wäre, dass der größere der beiden Achsenwertbeträge auch gleich dem Betrag des Auslenkungsvektors entspricht. Damit ergäbe sich der Auslenkungsvektor als normalize(rect) * max(abs(rect.x), abs(rect.y)).
Re: GamePad-Werte in korrekten Kreis umrechnen
Verfasst: 12.04.2013, 13:52
von Schrompf
Gute Idee! Ich war gerade dabei, die Achse mit dem größeren absoluten Betrag irgendwie zu korrigieren, als ob der Betrag auf beiden Achsen präsent wäre... irgendwie so. Im Gegensatz zu Deinem Vorschlag ist die Idee aber ziemlich indirekt. Danke!
Re: GamePad-Werte in korrekten Kreis umrechnen
Verfasst: 12.04.2013, 13:59
von Alexander Kornrumpf
Etwas unausgegoren:
Fürs Rechnen nehme ich mal an maximale Auslenkung sei 0.5
Für Winkel phi zwischen Pi/4 und Pi/2 gilt bei maximaler Auslenkung also
x_max = 0.5 = r sin(phi)
oder auch (sinus ist dort streng positiv)
r_max(phi) = 0.5/sin(phi)
Dagegen ist die maximale Auslenkung r_kreis bei einem Kreis logischerweise konstant.
Du könntest nun für alle Paare r und phi einfach r' = r(r_kreis/r_max(phi)) skalieren.
Ich bin allerdings zu faul das für die restlichen Oktanten auch noch herzuleiten.
Re: GamePad-Werte in korrekten Kreis umrechnen
Verfasst: 12.04.2013, 14:26
von Schrompf
Zuerst nochmal Danke: Die Korrektur funktioniert wie erhofft, die Richtung auf dem Bildschirm hat jetzt deutlich mehr als vorher mit der Richtung des GamePad-Sticks gemeinsam.
Leider hat das GamePad toten Stellen in den vier diagonalen Hauptrichtungen. Da geht noch irgendwas anderes intern vor, so dass ich Wertänderungen in den vier Ecken gar nicht gemeldet bekomme. Und falls das als Ärger noch nicht reicht, werfen wir auch noch ein bisschen Signalverlust mit in die Gleichung: wenn man mit dem Stick ganz fix in die gegenüberliegende Auslenkung wechselt, geht diese Änderung manchmal verloren und man bekommt immernoch die alten Werte übermittelt. Ja so eine Freude.
Re: GamePad-Werte in korrekten Kreis umrechnen
Verfasst: 12.04.2013, 17:33
von Krishty
Ich würde auch Alexanders Lösung vorschlagen. An den Winkel kommst du ganz einfach mit atan2(y, x). Dann berechnest du, wie weit der Punkt des Einheitsquadrats in diese Richtung entfernt ist und teilst dadurch, um das Quadrat auf einen Kreis abzubilden – das ist Alexanders Formel. Wenn man jetzt noch beachtet, dass das atan2() ein Winkelverhältnis ist und der Sinus ebenfalls, kommt am Ende vielleicht noch eine blamabel simple Formel raus. Wenn es ganz blamabel wird, vielleicht sogar Cats.
Jedenfalls wollte ich noch anmerken, dass ich hier einen Joystick habe, der sich tatsächlich im Rechteck bewegt. Also mach bitte nicht, dass die Formel jetzt pauschal aktiv ist.
Re: GamePad-Werte in korrekten Kreis umrechnen
Verfasst: 12.04.2013, 18:11
von CodingCat
Krishty hat geschrieben:Ich würde auch Alexanders Lösung vorschlagen. An den Winkel kommst du ganz einfach mit atan2(y, x). Dann berechnest du, wie weit der Punkt des Einheitsquadrats in diese Richtung entfernt ist und teilst dadurch, um das Quadrat auf einen Kreis abzubilden – das ist Alexanders Formel. Wenn man jetzt noch beachtet, dass das atan2() ein Winkelverhältnis ist und der Sinus ebenfalls, kommt am Ende vielleicht noch eine blamabel simple Formel raus. Wenn es ganz blamabel wird, vielleicht sogar Cats.
Sogar ziemlich sicher, denn genau diese Überlegungen stecken dahinter. ;) Schlussendlich war meine Annahme, dass der Eingangsvektor nach Projektion auf das Einheitsquadrat mit dem Betrag des Eingangsvektors skaliert wird, um von einem Punkt im Kreis auf einen Punkt im Quadrat abzubilden. Genau das habe ich dann mit obiger Formel fix umgekehrt.
Re: GamePad-Werte in korrekten Kreis umrechnen
Verfasst: 12.04.2013, 18:19
von Alexander Kornrumpf
Kannst du, wenns nicht zuviel Mühe ist, mal ein Bild machen? Ich kapier es nicht so richtig. Alternativ auch etwas was mit Vektoren arbeitet und nicht mit dubiosen "rects".
Re: GamePad-Werte in korrekten Kreis umrechnen
Verfasst: 12.04.2013, 18:24
von CodingCat
Alexander Kornrumpf hat geschrieben:Kannst du, wenns nicht zuviel Mühe ist, mal ein Bild machen? Ich kapier es nicht so richtig. Alternativ auch etwas was mit Vektoren arbeitet und nicht mit dubiosen "rects".
rect ist doch ein Vektor, nämlich genau der Eingabevektor im Rechteck, den Schrompf beschreibt. Bild kommt.
Re: GamePad-Werte in korrekten Kreis umrechnen
Verfasst: 12.04.2013, 18:33
von Alexander Kornrumpf
CodingCat hat geschrieben:Alexander Kornrumpf hat geschrieben:Kannst du, wenns nicht zuviel Mühe ist, mal ein Bild machen? Ich kapier es nicht so richtig. Alternativ auch etwas was mit Vektoren arbeitet und nicht mit dubiosen "rects".
rect ist doch ein Vektor, nämlich genau der Eingabevektor im Rechteck, den Schrompf beschreibt. Bild kommt.
Mir ist jetzt glaube ich klar was du gemacht hast. Ob das dasselbe ist muss ich irgendwann in Ruhe herleiten.
Re: GamePad-Werte in korrekten Kreis umrechnen
Verfasst: 12.04.2013, 18:35
von CodingCat
Re: GamePad-Werte in korrekten Kreis umrechnen
Verfasst: 12.04.2013, 18:47
von eXile
CodingCat hat geschrieben:Eine naheliegende Möglichkeit wäre, dass der größere der beiden Achsenwertbeträge auch gleich dem Betrag des Auslenkungsvektors entspricht. Damit ergäbe sich der Auslenkungsvektor als normalize(rect) * max(abs(rect.x), abs(rect.y)).
Korrekt. Um etwas mathematischen Nährwert noch hinzuzufügen (siehe hierzu
dieses Bild):
- Projektion auf „Einheitsdiamant“: \($$\mathbf{v_p} = \frac{\mathbf{v}}{\|\mathbf{v}\|_1}$$\)
- Projektion auf Einheitskreis (das habt ihr schon hundertmal gemacht): \($$\mathbf{v_p} = \frac{\mathbf{v}}{\|\mathbf{v}\|_2}$$\)
- Projektion auf Einheitsquadrat (das wollen wir hier machen): \($$\mathbf{v_p} = \frac{\mathbf{v}}{\|\mathbf{v}\|_{\infty}} = \frac{\mathbf{v}}{\max \left(|v_1|, \ldots ,|v_n| \right)}$$\)
Das funktioniert so im Allgemeinen für beliebig viele Dimensionen, für beliebige
\($p \geq 1$\)-Normen und für alle Vektoren mit Norm ungleich 0.
Re: GamePad-Werte in korrekten Kreis umrechnen
Verfasst: 12.04.2013, 18:57
von Alexander Kornrumpf
eXile hat geschrieben:CodingCat hat geschrieben:Eine naheliegende Möglichkeit wäre, dass der größere der beiden Achsenwertbeträge auch gleich dem Betrag des Auslenkungsvektors entspricht. Damit ergäbe sich der Auslenkungsvektor als normalize(rect) * max(abs(rect.x), abs(rect.y)).
Korrekt. Um etwas mathematischen Nährwert noch hinzuzufügen (siehe hierzu
dieses Bild):
- Projektion auf „Einheitsdiamant“: \($$\mathbf{v_p} = \frac{\mathbf{v}}{\|\mathbf{v}\|_1}$$\)
- Projektion auf Einheitskreis (das habt ihr schon hundertmal gemacht): \($$\mathbf{v_p} = \frac{\mathbf{v}}{\|\mathbf{v}\|_2}$$\)
- Projektion auf Einheitsquadrat (das habt ihr schon hundertmal gemacht): \($$\mathbf{v_p} = \frac{\mathbf{v}}{\|\mathbf{v}\|_{\infty}} = \frac{\mathbf{v}}{\max \left(|x_1|, \ldots ,|x_n| \right)}$$\)
Das funktioniert so im Allgemeinen für beliebig viele Dimensionen, für beliebige
\($p$\)-Normen und für alle Vektoren mit Norm ungleich 0.
Da hell, das bringe ich sogar meinen Studenten bei. Also WiWis. Manchmal hat Mensch ein Brett vor dem Kopf.
Ich kann aber auch sagen warum: Früher in den MFC hieß NormalizeRect dafür zu sorgen dass die obere rechte Ecke eines Rechtecks tatsächlich über und rechter war als die untere linke (oder so ähnlich). Also (0,1),(1,0) -> (0,0),(1,1). Deswegen hat Cats Schreibweise bei mir das völlig falsche Mindset getriggert.
Aber da ich Polarkoordinaten nur einmal im Jahrzehnt benutze, werde ich zu meiner Erbauung trotzdem am WE die Äquivalenz von Kartesischer- und Polardarstellung des Sachverhalts nachweisen. Es ist zumindest ein schönes Hobby.
Re: GamePad-Werte in korrekten Kreis umrechnen
Verfasst: 12.04.2013, 19:25
von eXile
Ich habe das ganze mir noch mathematisch etwas genauer betrachtet, und bin zum Ergebnis gekommen, dass die obige Vorgehensweise für jede Funktion
\($f: \mathbb{R}^n \to \mathbb{R}$\) funktioniert, wobei für
\($f$\) gelten muss:
- \($f(\mathbf{x}) > 0$\) für \($\mathbf{x} \neq 0$\)
- \($f(\alpha \mathbf{x})=|\alpha| f(\mathbf{x})$\)
Das sind exakt die Bedingungen für eine Norm, nur ohne Dreiecksungleichung; diese brauchen wir hier nicht. Wenn wir unsere Projektion
\($$\begin{align}\mathbf{p}: \quad \mathbb{R}^n &\to \mathbb{R}^n, \\
\mathbf{p}(\mathbf{v}) &\mapsto \frac{\mathbf{p}}{f(\mathbf{p})}\end{align}$$\)uns dann anschauen, stellen wir fest:
\($$\mathbf{p}(\alpha \mathbf{x}) = \frac{\alpha \mathbf{x}}{f(\alpha \mathbf{x})} = \frac{\alpha \mathbf{x}}{|\alpha| f(\mathbf{x})} = \operatorname{sgn}(\alpha) \cdot \frac{\mathbf{x}}{f(\mathbf{x})} = \operatorname{sgn}(\alpha) \cdot \mathbf{p}(\mathbf{x})$$\)Auch wenn man es erstmal nicht glauben mag, so entspricht obige Formel genau unseren Vorstellungen: Wenn
\($\alpha$\) positiv ist, so ist
\($\mathbf{p}(\alpha \mathbf{x}) = \mathbf{p}(\mathbf{x})$\); dies ist genau die Projektionseigenschaft, dass Punkte auf Linien vom Nullpunkt aus alle auf den gleichen Punkt abgebildet werden. Das Signum da ist leider notwendig, weil wir bei einem negativen
\($\alpha$\) auf die andere Seite vom Nullpunkt aus gesehen abbilden wollen.
Durch den Verzicht auf die Dreiecksungleichung funktioniert das also auch in solchen Fällen: